GRADO 6° (MATEMÁTICAS) 2 PERIODO

GRADO 6°

MATEMÁTICAS

BIENVENIDOS

MATEMÁTICAS

Docente encargado
Duván Gamboa López

Un saludo fraterno

Por medio de éste espacio vamos a desarrollar los trabajos y las explicaciones correspondientes a las temáticas de matemáticas (P1).

El estudiante debe tener claro lo siguiente:

• El blog será una de las herramientas que junto a la plataforma de videollamadas grupales zoom y los correos electrónicos, servirán como medios de comunicación entre el profesor y los estudiantes, a través de los cuales se direccionarán las temáticas que conforman el primer periodo de MATEMÁTICAS.

   A continuación se estipulan las actividades que le corresponden a cada una de estas aplicaciones virtuales:

En el blog estarán las explicaciones de cada tema; estas explicaciones aparecerán en videos, audios, textos e imágenes diseñados por el docente encargado de acuerdo a lo que exija cada tema.

Así mismo, se colgaran las actividades a realizar y las fechas de presentación.

Por medio de Zoom trataremos las inquietudes que surjan luego de interactuar con las explicaciones y actividades propuestas en el blog. Aprovecharemos el espacio para realizar y responder preguntas puntuales relacionadas con lo propuesto en el blog.

En el correo se ubicarán las soluciones que los estudiantes darán a las actividades propuestas por el docente cumpliendo con las fechas de entrega estipuladas previamente. De igual forma, el docente determinará la nota correspondiente a la actividad.

6lcvduvan1@gmail.com

NORMAS

NORMAS A CUMPLIR EN LOS ENCUENTROS CON ZOOM

1. Ser puntual
2. Portar la camisa de la institución educativa (diario o educación física)
3. Ubicarse en un lugar adecuado para ingresar a la sala de reunión
4. Respetar la clase 100%
5. No utilizar los recursos de ZOOM (chat-levantar la mano-compartir pantalla y otros) para molestar.
6. Realizar las preguntas en los momentos adecuados respetando los espacios de los demás.
7. No estar en otras actividades mientras dure la reunión.
8. Ingresar con su nombre y apellidos a la sala (De lo contrario no sera admitido por el anfitrión)
9. Ingresar con la cámara encendida. (Obligatorio)

Durante las secciones en ZOOM realizaré preguntas a los estudiantes relacionadas con lo colgado en el blog previamente. (Tendré en cuenta la participación de cada estudiante)

• No todo el material que subiré va a ser actividades; también se encontrarán con explicaciones relacionadas con los temas que se están viendo.

• Las soluciones se trabajan en el cuaderno, se toman fotos y me envían las imágenes al correo  6lcvduvan1@gmail.com

Las inquietudes las pueden depositar en la barra de comentarios del blog o realizarlas en la reunión de zoom. No se usará el correo para hacer o responder preguntas.

att: DUVÁN GAMBOA LÓPEZ
DOCENTE ENCARGADO

BIENVENIDO

TEMAS DEL PRIMER PERIODO

1. PROPOSICIONES
2. Proposiciones simples y compuestas
3. Conjunción-disyunción-implicación-equivalencia
4. Cuantificadores
5.  CONJUNTOS (Operaciones entre conjuntos)
6. SISTEMAS DE NUMERACIÓN
7. Ecuaciones e inecuaciones

LOS TEMAS EN ROJO YA FUERON VISTOS EN LAS CLASES PRESENCIALES
Se realizaron los talleres respectivos y algunas evaluaciones.

En este momento estamos trabajando el tema de Conjuntos; En la ultima clase vimos las relaciones entre conjuntos, las cuales son:

• Inclusión
• Igualdad
• Disyunción
• Intersección
• Unión

Es importante decir que la relación "unión" no fue trabajada en clase. (Se abordará en estas clases virtuales).

Recordemos el tema trabajado en la ultima clase "Relaciones entre conjuntos" con el siguiente video.

Clase del 16 de marzo (6-1) y (6-3)
Clase del 17 de marzo (6-2) y (6-4)

Taller sobre relaciones entre conjuntos

1) Determina cuales de los siguientes conjuntos son iguales

A = (0,1,2,3,4,5)                              C = (1,2,3,6)

B = (Divisores de 9)                       D = (Divisores de 6)

E = (Un número menor que 6)


2) Analiza las imágenes y responde:

¿Se da la relación de inclusión?

En caso de darse, ¿que conjunto está incluido en el otro?

Realiza el diagrama correspondiente de la inclusión entre los conjuntos si existe.




     

¿Qué tipo de relación existe entre los conjuntos A y B?

Determínelos por extensión

3) Determina la relación entre los conjuntos indicados. Luego, realiza el diagrama de Venn de la relación entre ellos.

E = (Un animal carnívoro)                      F = (Oso polar, león, tigre)


4) Si todos los elementos de A pertenecen a B, pero no todos los elementos de B pertenecen a A, ¿Cual es la relación que existe entre ellos?


5) Si dos conjuntos tienen todos sus elementos en común, ¿como son los conjuntos? Realice un ejemplo y represéntelo en un diagrama de Venn.


6)Determina por extensión cada par de conjuntos y realiza el diagrama de Venn que representa la relación entre ellos:


a)  A = ( Un número par menor o igual a 16)                  C = (Una vocal de la palabra pacífico)

     B = ( Un divisor de 16)                                                  D = ( Una vocal de la palabra castillo)




 E = ( Un mes con 30 días)

F = ( Un mes del año)

 NOTA: El taller lo resuelven en sus cuadernos, luego le toman foto a la solución y envían las imágenes al correo : gamboaduvanlcv890703@gmail.com

Tienen plazo hasta el jueves 19 de marzo 2020. 12:00 pm

ÉXITOS

CLASE REALIZADA EL 19 DE MARZO DEL 2020 (JUEVES)

En esta oportunidad no se dejarán actividades, el objetivo de la clase es el de reforzar el concepto de conjunto con algunas imágenes y videos explicativos de mi parte.

Inicio de clase

Con la siguiente imagen recordemos algunos puntos importantes sobre conjuntos:

Analicemos el siguiente diagrama:

E = (Animales carnívoros)      F = ( león, tigre, oso polar)

Fecha de publicación del contenido (27 de abril del 2020)  Lunes.

Unión entre conjuntos                                                  

Podemos observar dos conjuntos; el conjunto A y el conjunto B.

El conjunto A = (1,2,3,4,5)

El conjunto B = (4,5,6,7,8,9)

A U B = (1,2,3,4,5,6,7,8,9)   

 Como se puede observar, los números 4 y 5 hacen parte de ambos conjuntos, aunque realmente la operación que se lleva a cabo es la unión ya que tomamos todos los elementos de A y los unimos con todos los elementos de B.

Vamos a observar el siguiente video que nos habla sobre la unión de conjuntos.

RECORDEMOS

Luego de ver el video sobre la unión de conjuntos recordemos algunas bases teóricas sobre el tema central. (CONJUNTOS)

En el próximo bloque trabajaremos la diferencia entre conjuntos.

Tarea:

Plantear tres situaciones cotidianas que impliquen la unión entre conjuntos.  Enviar al correo.

En el encuentro en ZOOM abordaremos estas situaciones.

DIFERENCIA ENTRE CONJUNTOS

 La diferencia entre los conjuntos A y B , es el conjunto formado por todos los elementos que pertenecen a A y no pertenecen a B. La diferencia entre A y B se simboliza A-B.

La diferencia entre los conjuntos A y B se representa dibujando los conjuntos de acuerdo con la relación que hay entre ellos y rayando la región de la gráfica donde s encuentran ubicados los elementos que están en A y no están en B.

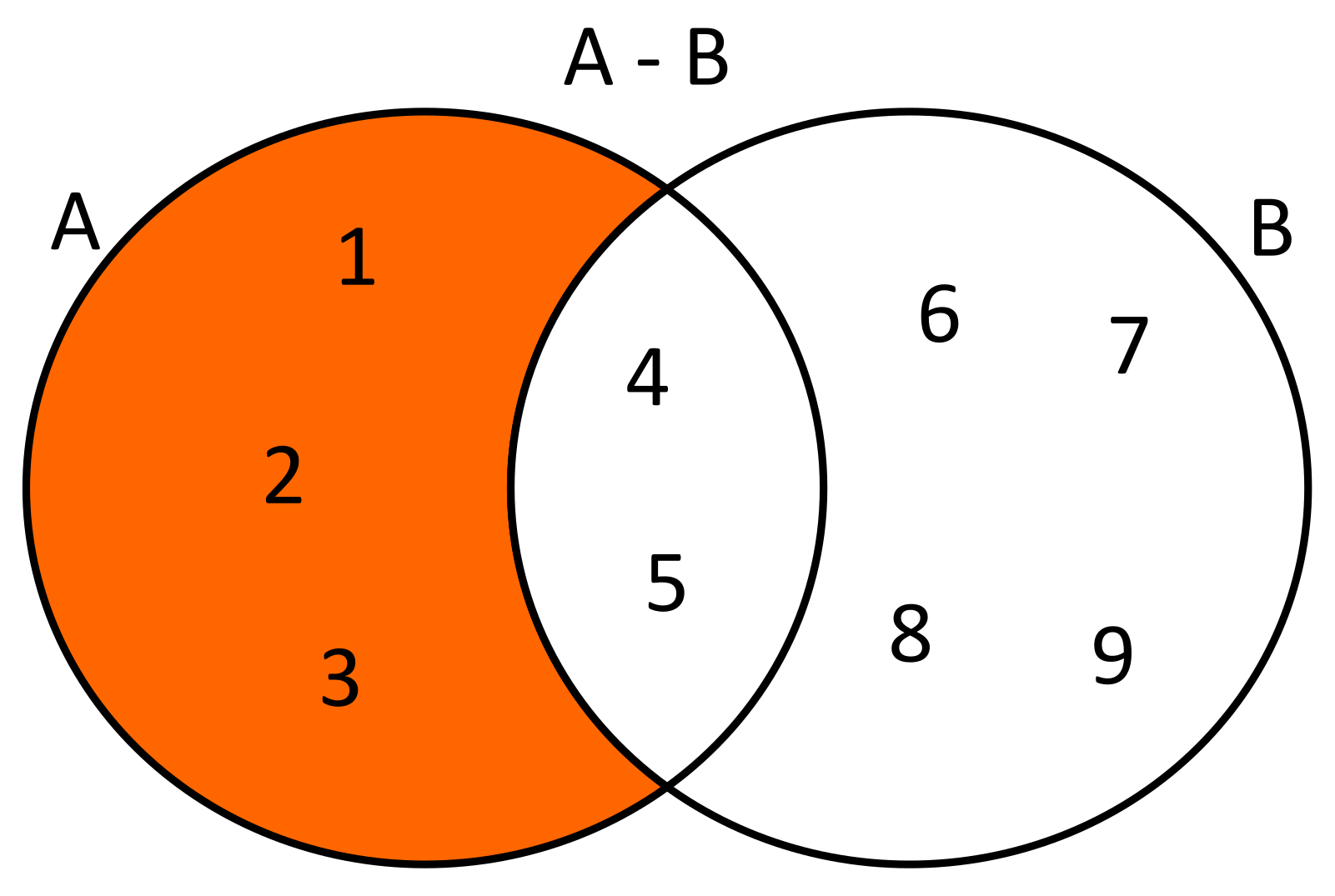Los elementos 1,2 y 3 son aquellos que solo le pertenecen al conjunto A. Por lo tanto, la región
sombreada representa la diferencia A-B.

EJEMPLO 1: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será B-A={6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

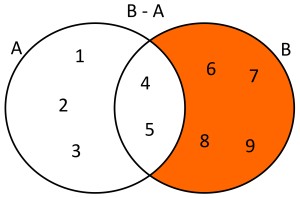La región sombreada indica la diferencia B-A.

EJEMPLO 2: Dados dos conjuntos F={x/x estudiantes que juegan fútbol} y B={x/x estudiantes que juegan básquet}, la diferencia de F con B, será F-B={x/x estudiantes que sólo juegan fútbol}. Usando diagramas de Venn se tendría lo siguiente:

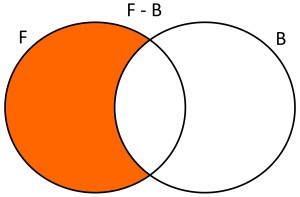
DIFERENCIA SIMÉTRICA

La diferencia simétrica entre los conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a la unión de A y B y no pertenecen a la intersección entre A y B. Se representa  A△B.

EJEMPLO 3: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

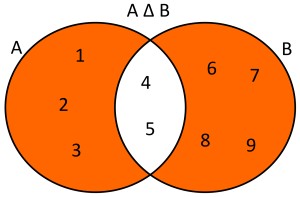
EN EL ENCUENTRO POR ZOOM ABORDAREMOS LAS INQUIETUDES QUE PUEDAN SURGIR.

09 de mayo del 2020

(SÁBADO)

Continuamos fortaleciendo la diferencia entre conjuntos y la diferencia simétrica entre conjuntos.

Diferencia entre conjuntos      A - B         

Diferencia simétrica entre conjuntos     A 

ACTIVIDAD A DESARROLLAR Y DEBATIR EN LA CLASE POR ZOOM

• A una fiesta asisten 27 personas. 12 Personas con gorro y 25 personas con antifaz. Si 10 personas tienen antifaz y gorro, ¿cuantas personas asistieron solo con gorro? ¿cuantas personas asistieron solo con antifaz?.

• Representa por medio de conjuntos la siguiente situación: Susana, carlos, andres, felipe, andrea y juan viven en el mismo edificio. Si susana, carlos y andrea viven en el mismo piso, ¿quienes no viven en el mismo piso?

Diferencia simétrica

• En un curso hay 80 personas, de las cuales, 45 estudian matemáticas, 36 estudian biología y algunos estudian las dos materias. ¿Cuantas personas solo estudian matemáticas o solo estudian biología?.

NOTA: 

Las soluciones de éstas actividades no se enviarán por el correo, se discutirán en el encuentro que tendremos por zoom. Si no logran resolverlas, no se preocupen, en la clase aclaramos dudas.

GRACIAS A TODOS.

14 de mayo del 2020

Taller sobre diferencia de conjuntos

Observar los videos para recordar algunos conceptos

Número (1)

Número (2)

A - B

Resolver cada uno de los puntos propuestos y enviar las soluciones al correo....

6lcvduvan1@gmail.com

1: A una sala de cine ingresan 68 personas. 23 ingresan con reloj y 37 con celular. si 12 ingresan con reloj y celular a la vez;

• ¿Cuantas personas ingresaron solo con reloj?
• ¿Cuantas personas ingresaron solo con celular?
• ¿Cuantas personas ingresaron a la sala al menos con celular o reloj?
• ¿Cuantas personas ingresaron a la sala sin celular  y sin reloj?

Represente la situación en diagrama sagital

2: Considere los siguientes conjuntos:

A = (3,4,5,6,7,8,9,10,11,12)        B = (3,6,9,12,15)              C = (2,4,6,10,14,16)

• Realice las operaciones     1: A-B              2: B-C         3: C -A        4:   A - C   

Realice para cada operación un diagrama sagital

3: Observe la imagen y realiza lo siguiente:

    

•  Indica la operación que se está realizando.
• ¿Que elementos conforman B - A?
• Representa los conjuntos por extensión y comprensión

4: Encuentra B - A

Tenga en cuenta que esto se refiere a los elementos de B que no están en A

• Sea A = { naranja, piña,  plátano,  manzana}

• Sea B = { naranja,  albaricoque,  piña,  plátano,  mango,  manzana}

5: Dado el diagrama, calcula:

• A - B = {                     }
• C -A =  {                      }   
• B - C = {                     }
• A - C = {                     }                           

6: Dado el diagrama, escribe f o v si la expresión es correcta o no:

• A - B = { 2,3,4 }  (   )
• B - A = { 6,7,8 }  (   )
• B - C = { 5,6,7 }  (   )
• A - C = { 2,3,4,5 }  (   )
• C - B = { 8,9,10 }  (   )

FECHA DE ENTREGA: MIÉRCOLES 20 DE MAYO HASTA LAS 8:00 pm.

Correo: 6lcvduvan1@gmail.com

22 de mayo del 2020 (VIERNES)

Lo mas pronto posible subiré algunos videos explicativos sobre el taller.

Continuamos con material para fortalecer la diferencia simétrica entre conjuntos.

Sean A y B dos conjuntos, entonces la diferencia simétrica se expresa 

Si observamos la operación de la imagen, podemos analizar que las regiones que se marcan son aquellas que contienen a los elementos no repetidos o que solo le pertenecen a uno de los conjuntos.

Retomemos el siguiente problema:

• En un curso hay 80 persona de las cuales, 45 estudian matemáticas, 36 estudian biología y algunos estudian las dos materias. ¿Cuantas personas solo estudian matemáticas o solo estudian biología?.

Solución:

Primero, dibuje un diagrama de Venn.

Segundo, se calcula el número de los que solo estudian matemáticas, así: 80 - 36 = 44, que es la diferencia entre el total y los que estudian biología.

Tercero, se calcula el número de los que solo estudian biología, así: 80 - 45 = 35, que es la diferencia entre el total menos los que estudian matemáticas.

Luego, los que estudian una o dos materias son:

MUB = 44 + 1 + 35 = 80. Los que estudian las dos materias son (1).

Por tanto, los que estudian una sola materia corresponden a 80 - 1 = 79. Entonces 79 personas estudian una sola materia.

Realizamos otro ejemplo:

Determinar la diferencia simétrica entre los conjuntos:

V = {Múltiplos de tres menores que 20}

R = {Múltiplos de dos menores que 20}

Primero, se determinan por extensión los conjuntos dados.

V = {3,6,9,12,15,18}

R = {2,4,6,8,10,12,14,16,18}

Segundo, se halla la unión entre los dos conjuntos.

V U R = {2,3,4,6,8,9,10,12,14,15,16,18}

Tercero, se halla la intersección entre los conjuntos.

{6,12,18} "Son los elementos que se repiten"

Por lo tanto la diferencia simétrica es:

{2,3,4,8,9,10,14,15,16}  "Son los elementos que no se repiten".

-------------------------------------------------------------

2 PERIODO

(01 DE JUNIO DEL 2020- LUNES)

DUVÁN GAMBOA LÓPEZ

Cel: 3186702849

e-mail: 6lcvduvan1@gmail.com

                

(Es importante tener en cuenta que todas las actividades deben enviarse únicamente a éste correo)

Blog: mirutavirtual2020.blogspot.com

Temas del segundo periodo

• Diferencia simétrica entre conjuntos
• Sistemas de numeración
• Sistema de numeración decimal
• Sistema de numeración binario
• Conjunto de los números naturales

Observa el siguiente vídeo explicativo

 

Último bloque sobre "Diferencia simétrica entre conjuntos"

Recordemos: La diferencia simétrica entre dos conjuntos A y B se representa:

Está conformada por todos los elementos que no son comunes entre A y B menos los elementos comunes entre ambos conjuntos.



Observemos el siguiente vídeo:

La siguiente imagen nos muestra una diferencia simétrica entre dos conjuntos; observa con atención:

Como puedes ver, las figuras que están en ambos conjuntos no se colocan en la diferencia simétrica. Solo se ponen los elementos no repetidos los cuales son en este caso (el rombo, el rectángulo, el triángulo y la estrella)

Realiza el siguiente ejercicio a modo de entrenamiento: (No debes enviarlo al correo, solo es para practicar. Si tiene dudas hable con el profesor).

Considera los conjuntos S y T

Realiza la diferencia simétrica entre ambos conjuntos

S = {números múltiplos de 5 menores o iguales a 40}

T = {números múltiplos de 4 mayores que 8 y menores o iguales a 40}

SISTEMAS DE NUMERACIÓN

Los sistemas de numeración han sido la respuesta que las diferentes culturas a través del tiempo han dado a la necesidad de contar.

A continuación presentamos tres de los sistemas de numeración más conocidos:

          Numeración egipcia                 Numeración China

Numeración maya

El conjunto de los simbolos y las reglas con las que ellos se combinan y operan se conoce como sistemea de numeración.

SISTEMA DE NUMERACIÓN DECIMAL

Actualmente es el sistema mas conocido y utilizado en el mundo.  También se conoce como sistema en base diez, el cual utiliza los símbolos 0,1,2,3,4,5,6,7,8,9 para escribir cualquier número.

El sistema de numeración decimal es posicional, es decir, que el valor que representa cada dígito depende de la posición que ocupa en el número.

EJEMPLO: En el número 4587 el dígito 5 representa quinientos, mientras que el dígito 8 representa ochenta.

Dentro del sistema de numeración decimal podemos representar un número en notación exponencial o en notación polinómica.

EJEMPLO:

Miremos el número 541328.

Podemos representarlo indicando la posición de cada dígito en el número.

5 CM

4DM

1UM

3C

2 D

8U

NOTACIÓN POLINÓMICA:

500000 + 40000 + 1000 + 300 + 20 + 8

NOTA: La notación exponencial se explicará en el encuentro por ZOOM al igual que todas las temáticas anteriores.

12 de junio del 2020

NOTACIÓN POLINÓMICA Y NOTACIÓN EXPONENCIAL

Como se expresó anteriormente, podemos representar un número de manera polinómica o de manera exponencial.

Miremos los siguientes números:

Notación polinómica

• 12.346 →  El número tiene cinco dígitos, los cuales de acuerdo a su posición asumen un valor dentro del número.
  
  

  1	2	3	4	6
  1 Decena de mil 10000	2 Unidades de mil 2000	3 Centenas 300	4 Decenas 40	6 Unidades    6

La notación polinómica indica la suma entre los números de cada casilla.

Por lo tanto, 12.346 = 10.000 + 2.000 + 300 + 40 + 6

• 437.893 →En este caso tenemos un número con seis dígitos, los cuales asumen un valor de acuerdo a su posición en el número; veamos:

4	3	7	8	9	3
4 Centenas de mil 400000	3 Decenas de mil 30000	7 Unidades de mil 7000	8  Centenas 800	9 Decenas 90	3 Unidades 3

En notación polinómica tenemos:

437.893 = 400.000 + 30.000 + 7.000 + 800 + 90 + 3

• 6,528.705 →En este caso tenemos un número de siete dígitos, los cuales asumen un valor de acuerdo a su posición en el número.

6	5	2	8	7	0	5
6 Unidades de millón 6000000	5 Centenas de mil 500000	2  Decenas de mil 20000	8 Unidades de mil 8000	7 Centenas 700	0 Decenas 00	5 Unidades 5

En notación polinómica tenemos:

6,000.000 + 500.000 + 20.000 + 8.000 + 700 + 00 + 5

Analice la siguiente imagen:

Notación exponencial

 

Para entender la notación exponencial es fundamental comprender lo que ocurre en la siguiente tabla:

POTENCIAS DE BASE 10

El exponente indica la cantidad de ceros que van a la derecha del uno (1)

28 DE JUNIO DEL 2020

SISTEMA DE NUMERACIÓN BINARIO

El sistema de númeración binario es el más fundamental sistema numérico que se utiliza en todas las computadoras. Cualquier dispositivo digital que vemos hoy en día, desde celulares hasta Smart TVs utilizan el sistema binario.

Este sistema sigue reglas muy similares al sistema decimal (el que usamos diariamente) pero en lugar de utilizar una base decimal de 10 números, se utiliza una base de 2 números, cero y uno (0 y 1). Es decir que los números van a ser expresados como una cadena de unos y ceros.

Convertir un número del sistema Decimal al sistema Binario.

Como el sistema binario solo tiene 2 alternativas 0 y 1; el número 2 se vuelve fundamental.

Para convertir un número decimal a su equivalente en binario entonces tenemos que comenzar a dividir por 2 hasta obtener restos de 1 y 0.

Por ejemplo si queremos convertir el número 152, debemos ir dividiendo el mismo por 2 como podemos ver en el siguiente cuadro: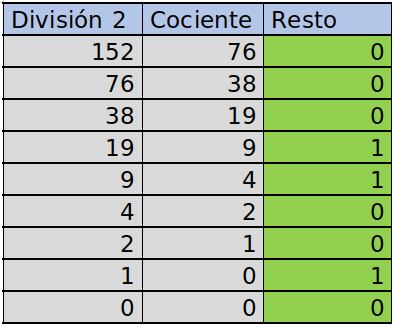

Una vez que completamos este proceso, simplemente tomamos los restos desde abajo hacia arriba y obtenemos el número binario equivalente, que en este caso es 10011000.

Convertir un número del sistema Binario al sistema Decimal.

Como en cualquier sistema de numeración, en los números binarios cada dígito tiene distinto valor dependiendo de la posición en que se encuentre dentro de la cadena. 

Para convertir un número binario en su equivalente en decimal, solamente debemos conocer las potencias de 2 y luego es cuestión de contar las posiciones. Algo a tener en cuenta es que al trabajar con binarios los algoritmos en general se aplican de derecha a izquierda.

Entonces, vamos a empezar a contar desde la derecha y a cada posición le vamos a asignar una potencia de 2 empezando por el 0. Por ejemplo, si queremos convertir el 10011000 al sistema decimal, deberíamos hacer lo siguiente:

MIREMOS OTROS EJEMPLOS

REPRESENTA EL NÚMERO 11110000 EN EL SISTEMA DECIMAL

5 CM

 4DM

1UM 

 3C

2 D

 8U

 1

2 

3 

4 

6 

 1 Decena de mil
10000

 2 Unidades de mil
2000

 3 Centenas
300

 4 Decenas
40

6 Unidades  
 6

 4

3 

7 

8 

9 

3 

 4
Centenas de mil
400000

 3
Decenas de mil
30000

 7
Unidades de mil
7000

 8 
Centenas
800

9 Decenas
90 

 3 Unidades
3

6 

 5

 2

 8

 7

 0

5 

6
Unidades de millón
6000000 

 5
Centenas de mil
500000

 2
 Decenas de mil
20000

8
Unidades de mil
8000 

 7 Centenas
700

 0 Decenas
00

 5 Unidades
5

 

03 de julio del 2020

viernes

CONTINUAMOS CON LOS SISTEMAS DECIMAL Y BINARIO.

Dentro de lo visto hasta el momento, hemos aprendido pasar un número del sistema decimal al binario y el caso contrario. En este bloque miraremos algunos ejemplos relacionados con lo anterior.

TABLA DE LAS POTENCIAS DEL NÚMERO 2

MIREMOS LOS SIGUIENTES VIDEOS SOBRE LAS CONVERSIONES. 

SON PARA FORTALECER LO VISTO CON EL PROFESOR.

DE DECIMAL A BINARIO

DE BINARIO A DECIMAL